Very little is known of Ptolemy's life. He most likely grew up in or near Alexandria, where he studied mathematics and astronomy. While he is most known for his work in mathematical astronomy, he wrote a number of other books that have survived, including Optics and Geography, which was an attempt to make a map of the world as known by Ptolemy with latitude and longitude measurements.
Ptolemy wrote the Almagest around 150 AD. The name Almagest actually comes from the latinized version of the Arabic name for his work, al-majisti, meaning "the greatest." The Greek name, Syntaxis, is short for its original title, The Mathematical Compilation.
With the Almagest, Ptolemy produced the first working, predicitve model of the solar system in the world, and was the culmination of Greek astronomy and the geocentric model. The Almagest was a complete textbook in mathematical astronomy, and was so successful that it became the standard in mathematical astronomy for 1400 years. The Almagest itself was broken into 13 chapters. He begins by teaching all the mathematics that is needed for the computations in the book, and then goes on to give detailed descriptions of how to make astronomical observations and mathematical models for the sun, moon and planets. He includes mathematical tables and star charts, and explains how to improve on observational data. He describes how to make any astronomical calculation that one may want. He improved on the work of Hipparchus, and produced the first complete working and predictive model of the solar system, and it was the basis for mathematical astronomy until the sixteenth century when Copernicus introduced his heliocentric model of the solar system. The Greek geocentric model is still often called the Ptolemeic system in honor of this achievement.
In addition to using epicycles to more accurately reflect the speed changes in the motion of the sun and moon, Ptolemy uses the epicycles introduced by Hipparchus to explain the retrograde motion of the planets. An epicycle is small orbit that carries a planet. The center of this little orbit is also itself going around the earth.
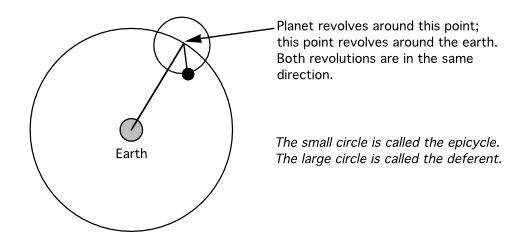
By playing with the sizes of the two circles, and their rate of rotation, one can make the planet appear to go backwards (when the planet is closest to the earth.) and so it can explain the retrograde motion of the planets. This also happens to explain why the planets are brighter during retrograde: they are closer to the earth. (The sun and moon never go backward in the sky, so those epicycles don't do that.)
There is a great shockwave file which I got from http://astro.unl.edu/naap/ssm/ssm.html. It shows the whole model, lets you adjust parameters and then runs so you can see what happens. Seeing it in action helps a lot.
Ptolemy's planetary model was based on eccentric epicycles, shown in the diagram to the right.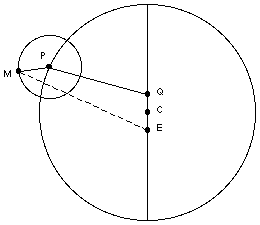
Each planet (lets say Mars in this case) travels around a little circle called an epicycle. In the diagram, let M be Mars and P be the center of the epicycle. The epicycle rotates at a constant angular speed. The center of the epicycle, P, also rotates around the earth on its own bigger circle, called the deferent, whose center is at point C. This model is called an eccentric epicycle because the center of the deferent, C, is not on the earth, E. This general layout was first conceived by Hipparchus, and Ptolemy makes it more accurate by adding the equant point, Q, such that CE = CQ. The center of the epicycle, P, does not rotate around the deferent at constant speed; rather it rotates in such a way that the line created by QP rotates with a constant angular speed. This causes the epicycle to travel faster or slower on the deferent. (Putting the earth off-center also makes it appear that the planet goes faster and slower, but Ptolemy needed the equant to make his model more accurately match the actual positions of the planets.) In later years, the equant becomes very controversial, as people claim that it violates the Principle of Uniform Circular Motion. (See the links at the bottom of the page for outside links with some animation of this process.)
In the Ptolemaic model, one only needs a few key pieces of information to predict where a planet is at any point in time. One needs to figure out the sizes of the epicycle and deferent, the eccentricity, the rotation rates, and the position of the planet at a particular date. Ptolemy not only gives all this information to the reader of his book, he explains how to make one's own observations and calculate what each parameter is. Given only 7 parameters, one can then calculate where a planet is at any point in time. It is important to note that this model worked reasonably well. In fact, it worked so well, that it was the standard model for almost 1400 years, until Copernicus proposes something else.
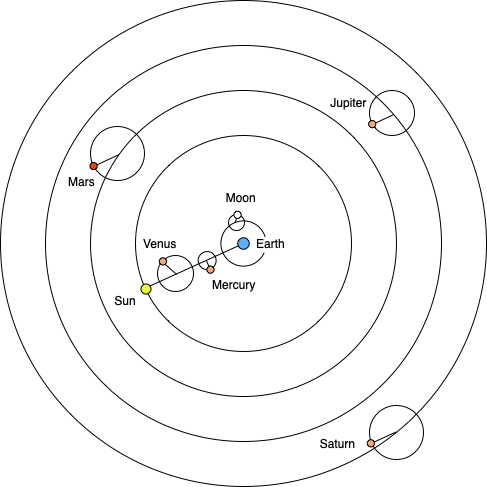
The diagram above shows the order of the planets in the Ptolemeic system. Note that if one switches the earth and the sun, then this matches the correct order of the planets. Ptolemy simply based this on the rates of the rotations. It should also be noted that the orbital parameters for each planet are independent of each other. Updating or improving the numbers for one of the planets has no effect on the other planets. Ptolemy simply chose orbital sizes so that the end of one orbit was the begining of the next. Also, notice that the orbits of Venus and Mercury were connected to the orbit of the sun. This is because these planets are never that far away from the sun in the sky.
The model described above was used to calculate the longitudinal position of the a planet along the ecliptic. However, the planets did not travel completely along the ecliptic, they traveled above and below it. Ptolemy uses a different model to be able to calculate the latitiude of the planet, which is the the angle above or below the ecliptic. The two models and parameters were independent of each other, but they combined to give a reasonably accurate (as far as the observational data went at the time) position for the planets.