Concepts
Miscellaneous
In a heliocentric model, there are several key positions of the planet around the sun. I'll draw the orbits as if they are circles, but it doesn't matter. All the terms refer to the position of the planet with respect to the sun, as seen from the earth.
Also, because someone always asks about angular measurements: A whole circle is broken up into 360 degrees. Each degree is then broken up into 60 minutes. Each minute is then broken up into 60 seconds. (So 1 second is the same as 1/3600 degree.) This is all a holdover from the Babylonian hexagecimal (base 60) number system from 5000 years ago.
For Superior Planets, the key positions are (1) opposition, (3) conjunction and (2 & 4) quadrature.
Hopefully, it is fairly clear that opposition (position 1) refers to when the sun and the planet are in opposite parts of the sky - that is to say, their positions along the ecliptic differ by 180
. Put another way, the angle of elongation of the planet is also 180. Only Superior Planets can be in opposition.
Conjunction means that two things are lined up - so in this case it means that the planet and the sun are at the same position along the ecliptic. For Superior Planets, this means the sun is in between the planet and the earth. Put another way, the angle of elongation of the planet is 0.
Quadrature refers to the two times when the planet is 90 away from the sun. Position 2 is the Eastern Quadrature because the planet is 90 to the east of the sun. Likewise, position 4 is Western Quadrature, because the planet is 90 to the west of the sun.
For inferior planets, the key positions are greatest elongations and conjunctions.
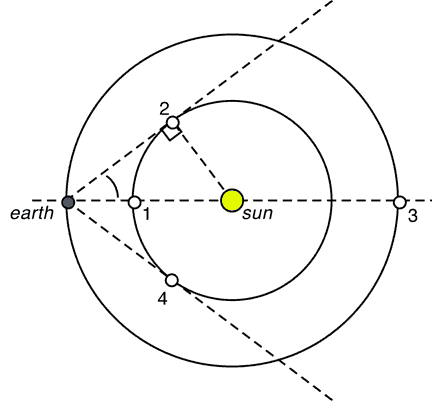
Positions 1 and 3 are both conjunctions. 1 is the Inferior Conjunction and 3 is the Superior Conjunction. In both cases, the sun and the planet are at the same position along the ecliptic.
Positions 2 and 4 are both called Greatest Elongations. While the angle of elongation for a superior planet can be anythign from 0 to 360, for an inferior planet there is a maximum angle, called the angle of greatest elongation. Notice that that angle will occur when the line from the earth to the planet is tangent to the planet's orbit. Position 2 is the Eastern and position 4 is the Western angle. Notice that when a planet is at its greatest elongation, we can easily calculate its distance to the sun because we have a right triangle with a hypoteneuse of 1 AU and a directly measureable angle.
This was also shown on Kepler's page, but for completeness, I'll show it here as well. Orbits are elliptical, with the sun (or a planet in the case of moons) at a focus.
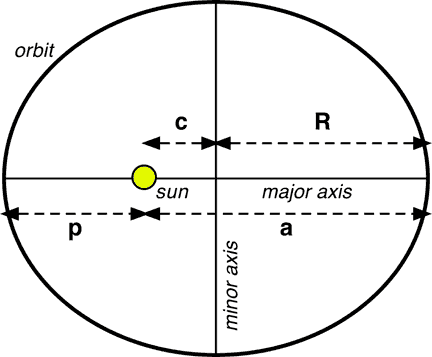
There is nothing at the other focus, and there is no special meaning to that point in space. In the diagram, the center of the orbit is where the two axis cross, and the sun is on the major axis. The other letters are:
c is distance from the center of the orbit to the sun, which is at the focus.
R is the semi-major axis. (Remember that "semi" meand half so it is half the major axis.) The semi-major axis is also the average distance of a planet to the sun, and is the key component to determining orbital periods.
p is perihelion, the closest the planet will come to the sun. Notice that this on on the major axis. Notice also that p = R - c.
a is aphelion, the farthest the planet will be from the sun. Again, notice that this is on the major axis. Notice also that a = R + c.
.